El problema de los 3 cuerpos

El problema de los 3 cuerpos ha fascinado a la humanidad durante siglos, sin una solución fiable, de forma cerrada y eficiente encontrada hasta la fecha. Ha trascendido a los mejores matemáticos y físicos del mundo, teniendo consecuencias reales en nuestras misiones de maniobras orbitales y puesta de satélites en órbita. Ha sido discutido en libros y más recientemente en la serie de Netflix. Veremos de dónde sale, como podemos intentar resolverlo, su aplicación en un caso real y casos especiales.

$n$-cuerpos

El problema de los $n$-cuerpos en física, concretamente astronomía, se refiere al problema matemático de determinar el movimiento de un grupo de $n$ cuerpos celestes en el futuro, al interactuar entre sí, siguiendo las leyes de la gravitación universal de Newton, tomando en cuenta sus masas, posiciones y velocidades iniciales. Es fundamental para la mecánica celeste, astrofísica y sistemas dinámicos.

Conociendo las posiciones iniciales de la órbita de un planeta, Newton produjo de manera analítica ecuaciones que permitían predecir el movimiento de dicho planeta utilizando geometría analítica. Sin embargo, con el paso de los años se dio cuenta que esas ecuaciones no modelaban correctamente las órbitas. Es entonces cuando se da cuenta que las fuerzas gravitacionales entre todos los planetas y cuerpos afectaban sus órbitas.

Por lo tanto, no basta con conocer sólo la posición y velocidad inicial de los cuerpos, si no también de las fuerzas gravitacionales interactuando entre sí, estirando y aflojando las órbitas, por lo tanto el problema fue formulado inicialmente a inicios del siglo XVII, aunque con una formulación errónea.

Desde sus inicios, fue considerado como un problema muy difícil y retador, ofreciéndose a partir del siglo XIX una recompensa para cualquiera que encontrara una solución general al problema por parte del rey de Suecia.

Para $n = 2$, el problema de los 2 cuerpos se resuelve de manera analítica, usando las ecuaciones de las leyes del movimiento de Newton y de gravitación universal, permitiendo describir a sistemas como el Sol y la Tierra a la perfección. Sin embargo, conforme $n$ crece, el problema es imposible de resolver de manera analítica debido a la naturaleza no lineal del sistema, por lo que hay que recurrir a soluciones numéricas, producto de algoritmos y métodos numéricos que inducen errores.

Para cada paso del método, hay que calcular $\frac{n(n-1)}{2}$ interacciones de las fuerzas entre cada par, exhibiendo comportamiento caótico, en donde ligeros cambios en las condiciones iniciales propician salidas diferentes, mientras $n$ sea más grande, más difícil y propenso a errores será de resolver el problema.

Formulación del problema de los 3 cuerpos

Lógicamente, la progresión del problema continúa con $n = 3$, siendo el problema de los 3 cuerpos estudiado por Euler inicialmente. Existen muchos casos especiales o restringidos del problema de los 3 cuerpos para los cuales podemos intentar resolver mucho más fácil, pero para la formulación general no hay ningun método de solución preferido.

Para $n = 3$, definimos 3 vectores de posición inicial $\vec{r_1}, \vec{r_2}, \vec{r_3}$ y 3 vectores de velocidad inicial $\vec{v_1}, \vec{v_2}, \vec{v_3}$ para cada cuerpo, cada uno en función de un tiempo $t$.

La Segunda Ley de Newton afirma que la fuerza en un cuerpo es igual a su masa por aceleración $F = ma$. Dado a que la aceleración es la segunda derivada de la posición con respecto al tiempo (movimiento), para cada cuerpo $i$ obtenemos la siguiente ecuación:

Por último, la Ley de Gravitación Universal entre dos cuerpos $i$ y $j$ esta dada por la siguiente ecuación, siendo $G$ la constante de gravitación (6.67430(15)×10−11):

Entonces, el sistema de ecuaciones diferenciales ordinarias que describe a todo el sistema es el siguiente:

Este sistema es de segundo orden debido a que usa la aceleración como derivada. El lado derecho suma las fuerzas gravitacionales de todos los cuerpos actuando en el cuerpo $i$, dividido por el cubo de la distancia porque el vector de fuerzas es sensible a la dirección, normalizandolo. De este sistema se desprenden nueve ecuaciones diferenciales, siguiendo una formulación newtoniana, aunque también se puede formular con el Hamiltoniano.

Para resolver el sistema de ecuaciones, convertiremos dicho sistema a un sistema de primer orden, definiendo a la velocidad como la primera derivada de la posición y reescribiendo todo el sistema en base a esa definición:

Aquí, $\vec{v_i}$ es el vector de velocidad del cuerpo $i$. La primera ecuación define a dicha velocidad y la segunda la aceleración, expresada en términos de velocidad (primera derivada).

Para cada cuerpo celeste, tenemos dos conjuntos de ecuaciones diferenciales de primer orden, una describe su posición a lo largo del tiempo (velocidad) y la otra describe como esa velocidad cambia con respecto al tiempo (determinada por las fuerzas gravitacionales actuando en el cuerpo).

Teniendo un sistema de primer orden, ahora podemos resolverlo usando métodos numéricos de ecuaciones diferenciales.

Runge Kutta de cuarto orden

El método Runge-Kutta toma este sistema de EDO de primer orden y calcula iterativamente las posiciones y velocidades de los cuerpos en cada paso temporal, mejorando la estimación de la solución en cada paso mediante cálculos intermedios (los valores «K» en la formulación Runge-Kutta).

Al resolver el sistema de EDO de manera numérica, damos pequeños pasos incrementales de tiempo ($\Delta t$), calculando el estado del sistema en cada paso. Empezamos con las condiciones iniciales, calculamos las fuerzas de interacción en el cuerpo, obtenemos las aceleraciones, actualizamos velocidades en base a la aceleración y actualizamos posiciones en base a la velocidad, repetimos, hasta que hayamos alcanzado el tiempo deseado.

Usaremos el paquete de DifferentialEquations para llamar al método numérico de Runge Kutta de 4to orden. Si bien podemos implementar nuestra propia versión del método, es mejor usar una definición probada y comprobada.

Para una EDO de la forma $\dfrac{dy}{dt} = f(t, y), y(t_0) = y_0$ donde $y(t)$ es la función desconocida del tiempo $t$, $f(t, y)$ la función dada y $y_0$ la condición inicial en el tiempo $t_0$, la meta es encontrar el valor de $y$ en un tiempo $t = t_0 + h$, donde h es el tamaño del paso, Runge Kutta de 4to orden aproxima a $y(t_0 + h)$ usando los siguientes pasos:

1. Calcula la primera pendiente en $k_1$ al inicio del intervalo usando la condición inicial: $k_1 = h \cdot f(t_0, y_0)$

2. Calcula la segunda pendiente en $k_2$ a la mitad del intervalo usando $y_0 + \frac{1}{2}k_1$ como el valor intermedio de $y$ en $t_0 + \frac{1}{2}h$: $k_2 = h \cdot f(t_0 + \frac{1}{2}h, y_0 + \frac{1}{2}k_1)$

3. Calcula la tercer pendiente en $k_3$ también a la mitad del intervalo pero usando a $y_0 + \frac{1}{2}k_2$ como la aproximación: $k_3 = h \cdot f(t_0 + \frac{1}{2}h, y_0 + \frac{1}{2}k_2)$

4. Calcula la cuarta y última pendiente en $k_4$ al final del intervalo, usando a $y_0 + \frac{1}{2}k_3$ como la aproximación de $y$ en $t_0 + h$: $k_4 = h \cdot f(t_0 + h, y_0 + k_3)$

5. Combina estas pendientes para obtener la aproximación final de $y(t_0, h)$: $y(t_0, h) \approx y_0 + \frac{1}{6}(k_1 + 2k_2 + 2k_3 + k_4)$

La Tierra, Marte y el Sol

Podemos resolver el problema de los 3 cuerpos para el sistema dado por el Sol, la Tierra y Marte, definiendo primero constantes y condiciones iniciales de velocidad, posición y masa, estando los cuerpos en conjunción (siendo la distancia máxima entre los cuerpos), reduciendo el sistema a un plano cartesiano con $x$ e $y$, sin tomar en cuenta $z$ (para simplificar más el problema).

La Tierra está aproximadamente a 149.6 millones de kilómetros del Sol, lo cual se define como una Unidad Astronómica de distancia. Marte orbita en promedio a 227.9 millones de kilómetros del Sol, o 1.52 UA. Sus velocidades son tangenciales a sus órbitas en el eje $y$, la Tierra orbitando en promedio a 30 km/s y Marte a 24 km/s. El Sol es colocado en el origen y sin moverse, debido a que su velocidad relativa con respecto a la Tierra y Marte es nula. Las masas son las masas reales de los cuerpos en kilogramos.

tspan = (0.0, 3.15567e7*3) # 3 años en segundos
UA = 1.496e11  # Unidad Astronómica de distancia en metros
velocity_earth = 29.78e3  # Velocidad orbital de la Tierra en m/s
velocity_mars = 24.07e3  # Velocidad orbital de Marte en m/s
mass_sun = 1.989e30  # Masa del Sol en kg
mass_earth = 5.972e24  # Masa de la Tierra kg
mass_mars = 6.417e23  # Masa de Marte en kg
masses = [mass_sun, mass_earth, mass_mars]
u0 = [
    0.0, 0.0,                     # r_sun (Sol en el origen)
    UA, 0.0,                      # r_earth (Tierra a  1 UA en el eje x, 0 en y)
    -1.52 * UA, 0.0,              # r_mars (Marte a 1.52 UA en el eje x opuesto, 0 en y)
    0.0, 0.0,                     # v_sun (El sol esta estacionario)
    0.0, velocity_earth,          # v_earth (Velocidad de la Tierra en el eje y, positivo, 0 en x)
    0.0, -velocity_mars           # v_mars (Velocidad de Marte en el eje y, negativo, 0 en x)
]

Ahora tenemos que definir nuestra ecuación diferencial y el código que calcule y actualice las fuerzas de interacción:

function three_body_problem!(du, u, p, t)
    # Constante Gravitacional en m^3/kg/s^2
    G = 6.67430e-11 
    # Posiciones y velocidades
    x₁, y₁, x₂, y₂, x₃, y₃ = u[1], u[2], u[3], u[4], u[5], u[6]
    # Masas
    m1, m2, m3 = p
    
    # Calculamos distancias euclidianas entre cada par de cuerpos
    r₁₂ = √((x₁ - x₂)^2 + (y₁ - y₂)^2)
    r₁₃ = √((x₁ - x₃)^2 + (y₁ - y₃)^2)
    r₂₃ = √((x₂ - x₃)^2 + (y₂ - y₃)^2)
    
    # Calculamos los vectores unitarios para las direcciones de las fuerzas
    ux₁₂, uy₁₂ = (x₂ - x₁) / r₁₂, (y₂ - y₁) / r₁₂
    ux₁₃, uy₁₃ = (x₃ - x₁) / r₁₃, (y₃ - y₁) / r₁₃
    ux₂₃, uy₂₃ = (x₃ - x₂) / r₂₃, (y₃ - y₂) / r₂₃
    
    # Fuerzas gravitacionales
    Fx₁₂, Fy₁₂ = G * m1 * m2 / r₁₂^2 * ux₁₂, G * m1 * m2 / r₁₂^2 * uy₁₂
    Fx₁₃, Fy₁₃ = G * m1 * m3 / r₁₃^2 * ux₁₃, G * m1 * m3 / r₁₃^2 * uy₁₃
    Fx₂₃, Fy₂₃ = G * m2 * m3 / r₂₃^2 * ux₂₃, G * m2 * m3 / r₂₃^2 * uy₂₃
    
    # Fuerzas netas
    Fx₁ = Fx₁₂ + Fx₁₃
    Fy₁ = Fy₁₂ + Fy₁₃
    Fx₂ = -Fx₁₂ + Fx₂₃
    Fy₂ = -Fy₁₂ + Fy₂₃
    Fx₃ = -Fx₁₃ - Fx₂₃
    Fy₃ = -Fy₁₃ - Fy₂₃

    # Actualizamos velocidades y posiciones
    du[1], du[2] = u[7], u[8]
    du[3], du[4] = u[9], u[10]
    du[5], du[6] = u[11], u[12]
    du[7], du[8] = Fx₁ / m1, Fy₁ / m1
    du[9], du[10] = Fx₂ / m2, Fy₂ / m2
    du[11], du[12] = Fx₃ / m3, Fy₃ / m3
end

Primero, obtenemos las posiciones en $x, y$ de cada cuerpo ($1 ... 3$) así como sus velocidades y masas.

Posteriormente, calculamos la distancia Euclidiana entre cada par de cuerpos, es decir, del cuerpo 1 al 2 ($r_{12}$), del 1 al 3 ($r_{13}$) y del 2 al 3 ($r_{23}$), con la fórmula de $r_{ij} = \sqrt{(x_i - x_j)^2 + (y_i - y_j)^2}$.

Luego, calculamos los vectores unitarios de las fuerzas para cada par de cuerpos, para determinar la dirección (no magnitud, por eso son unitarios) de las fuerzas entre un cuerpo y otro. Por ejemplo, para el vector unitario $\hat{ux_{1, 2}}$ calculamos el vector entre los dos cuerpos ($x_2 - x_1$), luego la magnitud (dada por el vector $\vec{r_{12}}$) y normalizamos al dividir el vector por su magnitud, esto para todas las fuerzas en todas las direcciones.

Utilizando la definición de la Ley de Gravitación Universal, calculamos para cada par de cuerpos, su fuerza entre sí.

La fuerza es dada por

Hemos calculado el vector unitario de cada cuerpo al otro, obteniendo la dirección de dicha fuerza. Al multiplicar la magnitud de la fuerza por dicho vector, obtenemos el vector de fuerza: $\vec{F_{ij}} = F_{ij} \cdot (\hat{ux_{ij}}, \hat{uy_{ij}})$

Conociendo todas las fuerzas gravitacionales que actúan en el cuerpo, hacemos la suma de fuerzas netas para cada objeto, para cada uno de sus ejes. Es importante ver cómo para 3 cuerpos y 2 ejes dimensionales, hay 3 interacciones por cuerpo para cada eje ($3 = \frac{3(3-1)}{2}$).

Por último, actualizamos la posición en base a la velocidad y la velocidad en base a la aceleración (por eso $a = F/m$), integrando numéricamente para pequeños pasos en el tiempo, es decir $r_1 = r_0 + v \cdot \Delta t$.

Esta función la ejecutaremos durante un número de pasos dado para el tiempo que deseemos, en este caso, tres años completos representados en segundos, para ver 3 revoluciones de la Tierra.

using DifferentialEquations
# Creamos el problema de ecuacion diferencial ordinaria
prob = ODEProblem(three_body_problem!, u0, tspan, masses)
# Resolvemos con RK4
sol = solve(prob, RK4(), dt=1.0e-1; abstol=1e-9, reltol=1e-9, maxiters=1e6) # dt es el paso de tiempo, h

De esta forma, usamos la definición de nuestro sistema y las condiciones iniciales para ser resueltas por el método de Runge Kutta de 4to orden, usando pasos de tiempo de 0.1, es decir, se calcularán las condiciones del sistema cada 0.1 pasos, hasta que cumplamos con el tiempo total dado, recordando que son tres años. Resolvemos y obtenemos los resultados, graficando el movimiento y la posición de los cuerpos, creando una animación

using Plots
x1_arr, y1_arr = [sol.u[i][1] for i in 1:length(sol.t)], [sol.u[i][2] for i in 1:length(sol.t)]
x2_arr, y2_arr = [sol.u[i][3] for i in 1:length(sol.t)], [sol.u[i][4] for i in 1:length(sol.t)]
x3_arr, y3_arr = [sol.u[i][5] for i in 1:length(sol.t)], [sol.u[i][6] for i in 1:length(sol.t)]
df = 5
default(bg=:black, grid=false, axis=false, size=(1920, 1080), legend=false)
line_colors = [:yellow, :blue, :red]
line_styles = [:dash, :dash, :dash]
transparency_levels = [0.8, 0.8, 0.8]

anim = @animate for i = 1:df:length(x1_arr)
    plot(x1_arr[1:i], y1_arr[1:i], linecolor=line_colors[1], linestyle=:dash, linewidth=2)
    plot!(x2_arr[1:i], y2_arr[1:i], linecolor=line_colors[2], linestyle=:dash, linewidth=2)
    plot!(x3_arr[1:i], y3_arr[1:i], linecolor=line_colors[3], linestyle=:dash, linewidth=2)

    scatter!([x1_arr[i]], [y1_arr[i]], color=line_colors[1], markersize=50,  markerstrokecolor=line_colors[1])
    scatter!([x2_arr[i]], [y2_arr[i]], color=line_colors[2], markersize=15,  markerstrokecolor=line_colors[2])
    scatter!([x3_arr[i]], [y3_arr[i]], color=line_colors[3], markersize=8,  markerstrokecolor=line_colors[3])
end
gif(anim, "anim_fps30_earth_sun_mars_colors_3years.gif", fps = 30)

Obteniendo como resultado, donde se aprecia a la Tierra completando su órbita con respecto al Sol 3 veces, 3 años, transcurriendo esos años mucho más lento en Marte:

Más Casos Especiales

Con este código funcionando, podemos probar diferentes condiciones iniciales, probando casos especiales del problema de los 3 cuerpos que han surgido a lo largo de los años, con órbitas periódicas. Hay que recalcar que ninguno de estos casos ocurriría naturalmente en la vida real, son producto de investigación de casos especiales de órbitas periódicas. La mayoría de los casos acaban en colisiones entre dos o más cuerpos o en el sistema desbaratándose por completo, con algún cuerpo escapando la influencia de los demás. El caso especial en el que los 3 cuerpos forman una órbita en forma de 8 Se forman 3 órbitas elípticas que se traspasan, caso de Broucke. El caso conocido como mariposa Los 3 cuerpos están en caída libre, atraídos uno por otro Masas desiguales producen órbitas gemelas en puntos opuestos de una órbita central

Es importante mostrar que cambios como la tolerancia numérica de los errores en el algoritmo afectan ampliamente, así como el algoritmo usado. 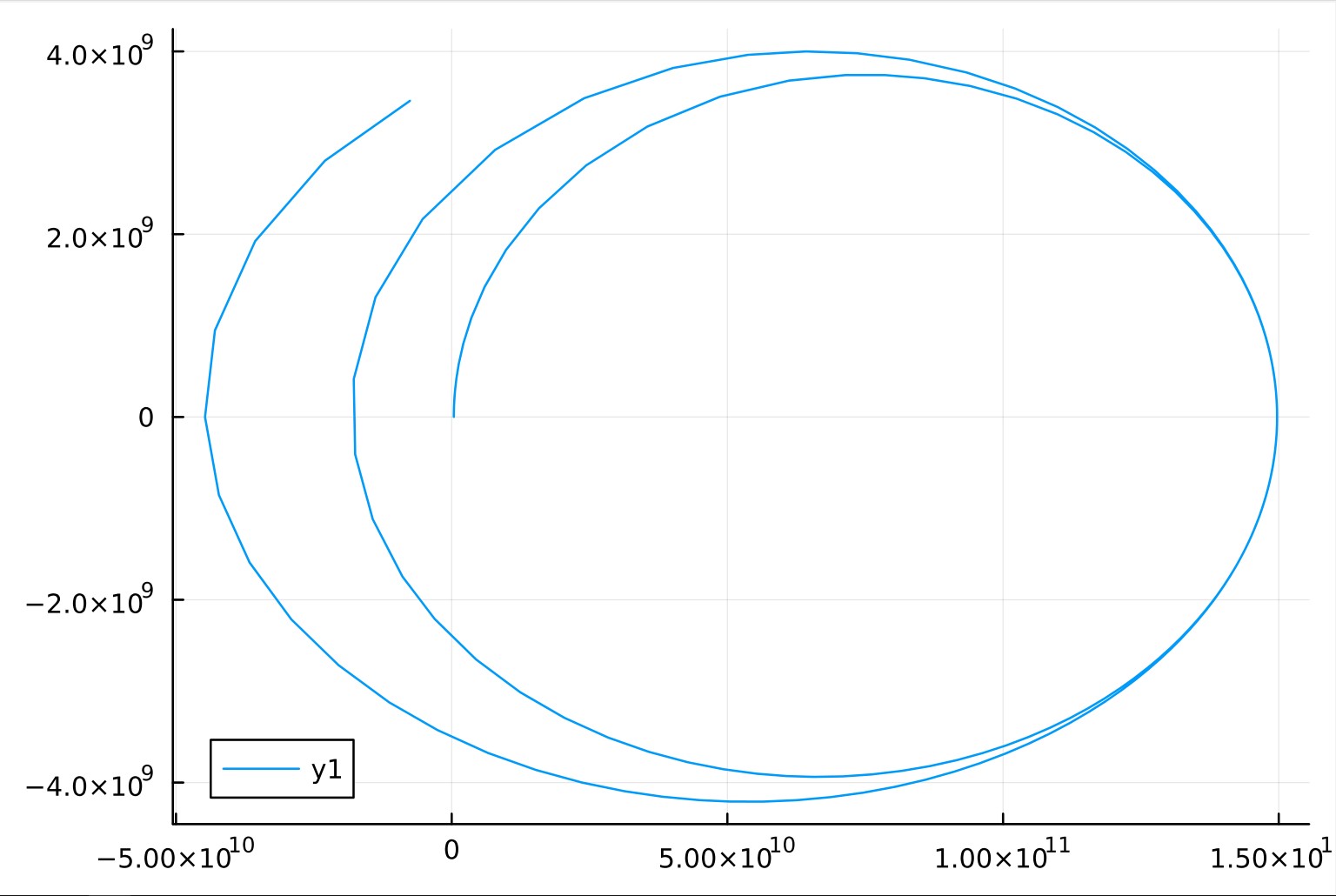Una tolerancia alta, propicia órbitas que degeneran más rápido y se alejan de la realidad 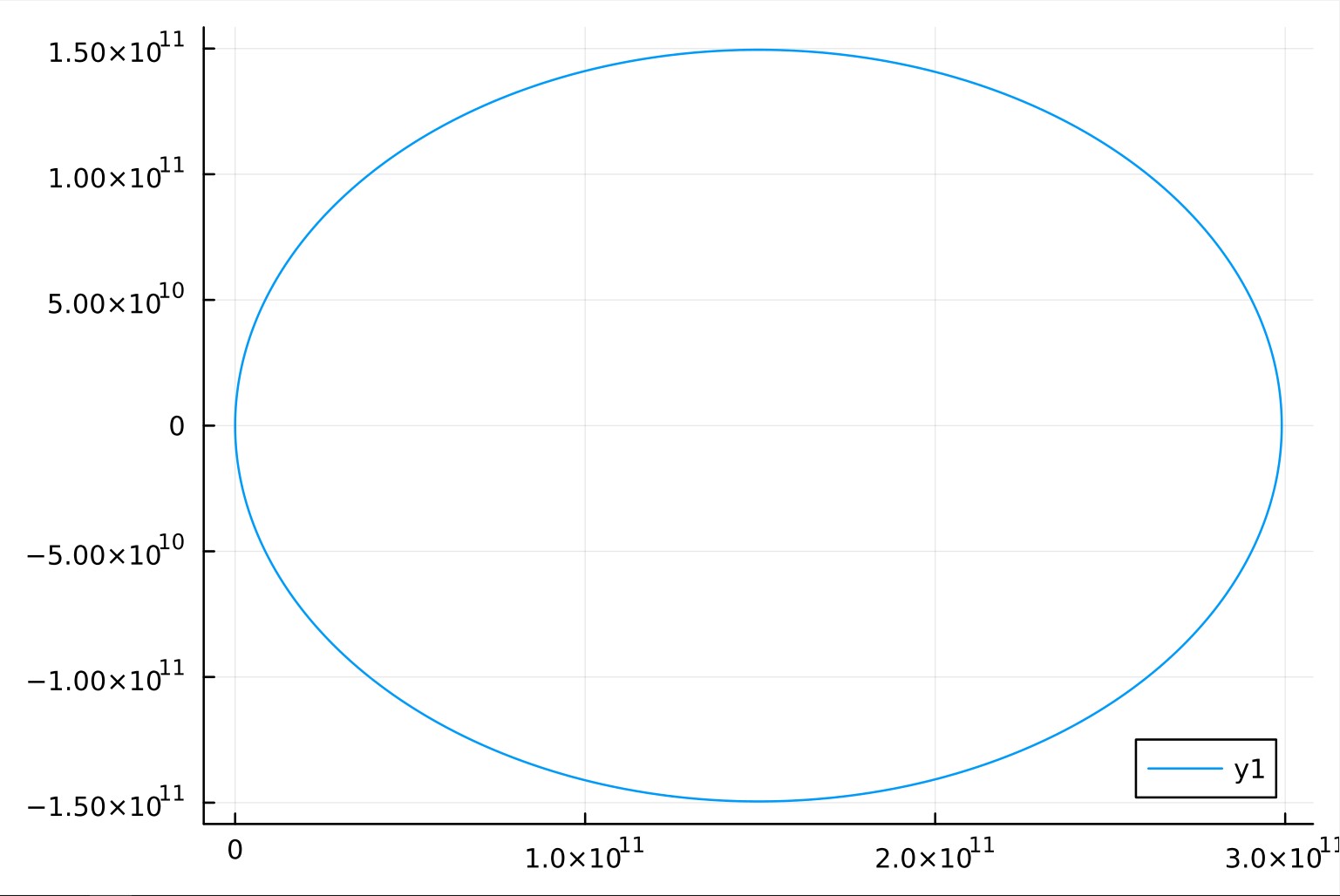Una tolerancia baja, da más precisión pero a expensas de mayor tiempo de cómputo

En este caso, decidí usar el método RK4, pero pudiendo haber usado uno distinto hubiera producido órbitas distintas también. Hay que recordar que es un problema de naturaleza caótica, extremadamente sensible a sus condiciones iniciales, un movimiento ligero en la posición inicial del cuerpo o una alteración en su vector de velocidad produciría órbitas completamente distintas e impredecibles.

En este caso, solo trabajamos con $n=3$, pero en el Sistema Solar tenemos 1 Sol, 8 planetas, 5 planetas enanos, 400 satélites naturales, 587,479 planetas menores, 3153 cometas y 19 satélites asteroidales. Con tan solo agregar un cuerpo más, para un problema de 4 cuerpos, las interacciones entre dichos cuerpos suman un total de 6 pares para cada cuerpo. Si tenemos cuatro ecuaciones diferenciales para cada cuerpo, dos describiendo posición y dos describiendo velocidad, necesitariamos un total de 16 ecuaciones en nuestro nuevo sistema.

Es evidente la complejidad computacional y algoritmíca por la que deben pasar todas las planeacion de misiones y maniobras para tomar en cuenta las interacciones gravitacionales entre los cuerpos que rodean a la Tierra. Para problemas de muchos cuerpos, no es viable evaluar la energía potencial de todo el sistema debido al número de cálculos, por lo que se usan algoritmos distintos, siguiendo la teoría de campo medio o simulaciones de partículas.

Una prueba más del ingenio de la humanidad al no rendirse antes las limitantes teóricas y matemáticas del universo en el que vivimos.

Referencias

R. Broucke, D. Boggs, On relative periodic solutions of the planar general three-body problem, Celest. Mech. 12, 439 (1975).

X. Li, Y. Jing, S. Liao, The 1223 new periodic orbits of planar three-body problem with unequal mass and zero angular momentum, Publications of the Astronomical Society of Japan, (2018).

X. Li, S. Liao, Collisionless periodic orbits in the free-fall three-body problem, New Astronomy (2019).

M. Šuvakov, V. Dmitrašinović, Three Classes of Newtonian Three-Body Planar Periodic Orbits, Phys. Rev. Lett. 110, 114301 (2013).

A. Chenciner, R. Montgomery, A remarkable periodic solution of the three-body problem in the case of equal masses, Annals of Mathematics. Second Series, 152 (3): 881–902 (2000).

H. Curtis, Orbital Mechanics for Engineering Students, Elsevier, (2020).

NASA, Planetary Fact Sheet, link.

R. Reusser, Periodic Planar Three-Body Orbits, link.